剛体の運動
目次
概要
質点は形や大きさを持たず、質量だけを持ち、その運動は位置と運動量で記述される。また質点の運動はNewtonの運動方程式を解くことで知ることができる。これに対して、剛体は形と質量の分布を持つ。剛体の運動は重心の位置と併進運動量、姿勢と角運動量で記述される。姿勢を表す方法は色々あり、例えば回転行列やオイラー角、四元数などがある。また質量の他に回転運動に関わる性質である慣性モーメントを持つ。剛体重心の併進運動は質点と同じくNewtonの運動方程式を用いて表され、回転運動はオイラーの運動方程式によって表される。
併進運動
まず剛体の重心を定義する。剛体中の任意の点の位置ベクトルをq とする。重心の位置ベクトルをqG とし、重心からq へのベクトルをs とする。
(1)
これらの関係を図に示す。
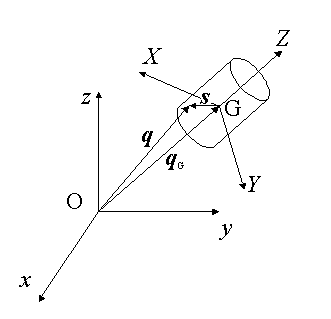
重心は以下のように定義される。
(2)
ここで右辺の積分は剛体領域中での体積積分である。
定義から以下の関係が成り立つ。
(3)
質点の運動方程式は
(4)
これを剛体の領域中で体積積分する。
(5)
(6)
(7)
(8)
併進運動の運動方程式が導かれる。
(9)
回転運動
ベクトルの外積の行列による表現
回転の運動方程式にはベクトルの外積が多く使われる。ベクトルの外積を行列を用いて表すことができ、便利なのでこれを導入する。
3次のベクトルa とベクトルb の外積は以下のように表される。
(5)
#の記号を導入し、a# は次のような反対称行列を示すこととする。
(6)
これを用いると外積は次のように表される。
(7)
一般的な関係
(8)
(9)
(10)
(11)
ここで
(12)
回転行列
ベクトルは基底を用いて表すことができる。
(13)
空間座標系における基底をe とする。
(14)
基底を回転させる行列をR' とする。
(15)
e'を基底とする新たな座標系でのベクトルq をq' とする。
(16)
(17)
ベクトルの座標系を変換する回転行列をR とすると
(18)
(19)
回転行列は転置行列が逆行列に等しいという性質を持つため
(20)
基底を変換する行列と、ベクトルの座標系を変換する行列とは逆行列の関係にある。
角速度ベクトル
角速度ベクトルの方向は回転軸と一致し、その絶対値はその回転軸まわりの角速度に等しい。速度と以下の関係にある。
(21)
慣性モーメント
慣性モーメントは3×3の行列で以下のように計算される。
(22)
また慣性モーメントは剛体の慣性主軸座標系では対角行列となり、主慣性モーメントと呼ばれる。空間座標系と慣性主軸座標系の慣性モーメントは以下の関係にある。
(23)
主慣性モーメントは対角行列なので
(24)
角運動量
角運動量は
(25)
また
(26)
の関係から、慣性モーメントを用いて表される。
(27)
慣性主軸系では
(28)
オイラー角
オイラー角とは三次元有限回転を表す方法のひとつで、3つの角度(θ, φ, ψ) から成る。オイラー角による三次元回転は次のような座標系の変換を示す。原点をO とし、右手系の座標系とする。
- 座標系O-xyz をz軸を回転軸として、右ねじの方向にφ 回転させる。回転後の座標系をO-x'y'z' とする。
- 座標系O-x'y'z' をx' 軸を回転軸として、右ねじの方向にθ 回転させる。回転後の座標系をO-x''y''z'' とする。
- 座標系O-x''y''z''をy'' 軸を回転軸として、右ねじの方向にψ 回転させる。回転後の座標系をO-x''y''z'' とする。
オイラー角(θ, φ, ψ) の変域は
(29)
である。
1、2、3の三つの回転による座標系の変換はそれぞれの回転行列の合成によって表される。
(30)
右辺を計算すると以下になる。
(31)
よってベクトルの座標系を変える回転行列R は
(32)
角速度との関係は以下から
(33)
(34)
(35)
が成り立つ。これを計算すると
(36)
オイラー角の時間微分について書くと
(37)
四元数
ここでは簡単のため四元数の詳しい性質についてはなるべく触れず回転行列とオイラー角との関係を述べる。任意の四元数を1つの実数と1つの3次ベクトル、Q0 とQ で表すこととする。
(38)
絶対値が1であるため
(39)
回転行列は
(40)
(41)
(42)
オイラー角との関係は
(43)
(44)
四元数の時間微分は
(45)
オイラーの運動方程式
トルクは以下のように表される。
(46)
角運動量の時間微分は
(47)
右辺第一項は0で、第二項は角速度との関係から
(48)
よって、
(49)
右辺を慣性主軸系の変数を用いて書き換えると、
(50)
参考にしたもの
- 有限要素法(FEM)のページ/剛体の運動
- http://ums.futene.net/wiki/Mech/rigid_body/index.html
- 上田 顯:分子シミュレーション −古典系から量子系手法まで−Molecular Simulation−from Classical to Quantum Methods−
- http://www.shokabo.co.jp/mybooks/ISBN978-4-7853-1534-4.htm
- ときわ台学/ベクトル解析/AppendixB2 慣性モーメント・オイラーの方程式
- http://www.f-denshi.com/000TokiwaJPN/20vectr/bpx02-momnt.html