圧力と応力
目次
圧力
連続体における圧力は単位面積に加わる力として定義されるが、粒子系においてこれは適用できない。粒子系における圧力は熱力学の関係から以下の式によって計算される。
(1)
ここでPは圧力、Eは内部エネルギー、Vは体積、Sはエントロピー、Nは粒子数、Tは温度、Fはヘルムホルツ自由エネルギーである。圧力は普通の場合は圧縮が正の値として定義される。
正準集合ではFは以下のように分配関数Zを用いて表される。
(2)
(3)
よって圧力はハミルトニアンを体積で偏微分した量の平均値として表される。ここで〈〉は平均値を示す。
(4)
粒子系の内部エネルギーはハミルトニアンの平均値に等しい。粒子系のハミルトニアンは以下のように表される。
(5)
ここでKは運動エネルギー、Φはポテンシャルエネルギー、paは粒子の運動量、raは粒子の座標を示す。座標と運動量を体積を用いて規格化し、ハミルトニアンを書き直すと
(6)
(7)
これを体積で偏微分し応力を求める式が得られる。
(8)
応力とひずみ
応力とひずみについては分野によって正負の定義が異なるため注意が必要である。岩盤力学の分野では多くの場合、圧縮応力と収縮ひずみを正の値、引張応力と膨張ひずみを負の値にとる。金属を扱う多くの分野ではこれとは逆に引張応力と膨張ひずみを正、圧縮応力と収縮ひずみを負の値にとる。また圧縮応力と膨張ひずみを正の値にとり、引張応力と収縮ひずみを負の値にとることもある。この場合には変形による仕事の符号が変わるため注意が必要である。本稿では圧縮応力と収縮ひずみを正の値、引張応力と膨張ひずみを負の値をとることとする。
ひずみ
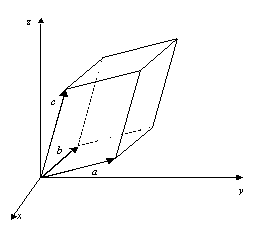
ひずみは巨視的な値として定義される。ひずみを定義するためには粒子系の形状を表す形状テンソルhを用いる必要がある。
hの成分は
(9)
である。ベクトルa,b,cとユニットセルの形状を図に示す。
ひずみは以下のように示される。
ここではεijはひずみテンソル、Gkmは計量テンソル、Iijは単位行列、Fijは変形勾配テンソルである。これはGreen-Lagrangeひずみテンソルにあたる。
(10)
(11)
(12)
応力
応力も圧力と似た方法によって定義される。熱力学の関係から以下のように示される。粒子数は変わらないこととする。
(13)
応力とひずみを用いて書き直すと以下のようになる。
(14)
ここでzijは第2Piola-Kirchhoff応力である。微小変形においてはひずみと応力の定義を厳密にする必要はないが、有限変形を扱う場合には第2Piola-Kirchhoff応力とGreen-Lagrangeひずみが用いられる。 ひずみの定義から
(15)
温度一定では
(16)
形状テンソルを用いて座標と運動量を規格化し、粒子系のハミルトニアンを書き直すと
(17)
(18)
(19)
ハミルトニアンを計量テンソルGで偏微分する。
(20)
以上より第2Piola-Kirchhoff応力とCaucy応力を計算する式が得られる。
(21)
(22)
(23)
参考にしたもの
- 慶應義塾大学理工学部物理学科 | 理論研究室のページ、能勢修一氏のノート、統計力学 (小正準集団の方法)
- http://www.phys.keio.ac.jp/guidance/labs/riron/riron-lab.html
- 東京大学大学院 強度信頼性工学研究室/泉聡志/主な論文リスト/博士論文
- http://www.fml.t.u-tokyo.ac.jp/~izumi/papers/index.htm