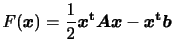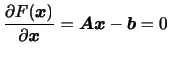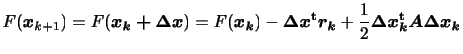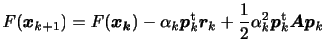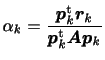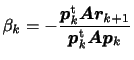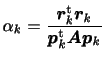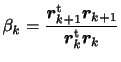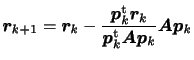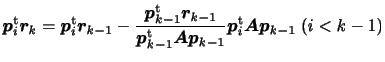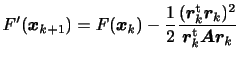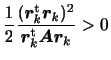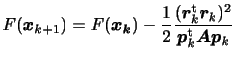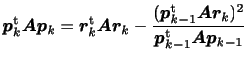共役勾配法 (Conjugate gradient method)
概要
共役勾配法は正値対称な連立一次方程式の反復解法として利用することができる。
連立一次方程式を以下のように表す。
ここで
正値とは![]() 以外の任意のベクトル
以外の任意のベクトル![]() に対して
に対して
![]() が成り立つことをいう。
が成り立つことをいう。
対称行列は転置しても元の行列と等しい行列で、
![]() が成り立つ。
が成り立つ。
また式(1)は式(2)の![]() を変数とする凡関数
を変数とする凡関数
![]() の最小値問題として表現することができる。
の最小値問題として表現することができる。
式(2)の最小値は![]() で偏微分することで得られ、
これは式(1)と一致する。
で偏微分することで得られ、
これは式(1)と一致する。
反復法による解の更新
式(1)の厳密解を
![]() からより厳密解に近い
からより厳密解に近い
![]() を得ることを考える。
を得ることを考える。
![]() を
を![]() を用いて、以下のように表す。
を用いて、以下のように表す。
式(2)から
次に![]() を修正量
を修正量![]() と修正方向ベクトル
と修正方向ベクトル![]() の積で表す。
の積で表す。
式(8)を![]() で偏微分し最小値をとる
で偏微分し最小値をとる![]() を得る。
を得る。
次に
![]() を求める必要がある。これには修正方向ベクトルの
を求める必要がある。これには修正方向ベクトルの
![]() に対する共役性が利用される。
また修正方向ベクトルの
に対する共役性が利用される。
また修正方向ベクトルの![]() に対する共役性から残差ベクトルは直交性を持つ。
これについては後で詳しく触れる。
この二つの条件は以下のように表される。
に対する共役性から残差ベクトルは直交性を持つ。
これについては後で詳しく触れる。
この二つの条件は以下のように表される。
![]() を
を
![]() と
と
![]() 、および
、および![]() を用いて表す。
を用いて表す。
式(13)に左側から
![]() をかけると次式が得られる。
をかけると次式が得られる。
![]() と
と
![]() の
の![]() に関する共役性から
に関する共役性から![]() が得られる。
が得られる。
![]() と
と![]() はさらに変形でき、以下のように表せる。
はさらに変形でき、以下のように表せる。
実際の計算手順
実際の具体的な計算手順を示す。これは以下のようになる。
- 初期条件
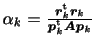
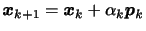
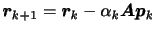
- もし残差が十分に小さければ繰り返し計算を終わる
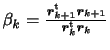
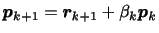
修正方向ベクトルのAに関する共役性と残差ベクトルの直交性
2では
![]() を決定する際に
を決定する際に
![]() と
と
![]() に関する共役性を持つように選んだ。
これによって、残差ベクトルが直交性を持つことを示す。
に関する共役性を持つように選んだ。
これによって、残差ベクトルが直交性を持つことを示す。
これに左側から
![]() をかけると
をかけると
の関係が得られる。
また式(13)の関係から修正方向ベクトルは残差ベクトルの線形和であり、
以下のように表現できる。
これに左側から
![]() をかけると式(19)が成り立つため
式(12)の残差ベクトルの直交性が示される。また
をかけると式(19)が成り立つため
式(12)の残差ベクトルの直交性が示される。また
の関係が得られる。
次に式(11)が成り立つことを示す。
式(18)に左側から
![]() をかける。
をかける。
であり、また
最急降下法との比較
共役勾配法は最急降下法よりも効率がよい方法であることを示す。
最急降下法では修正方向ベクトルとして残差ベクトルが選ばれる。
この関係を式(8)に代入すると以下の関係が得られる。
![]() が正値であることから
が正値であることから
が成り立ち、
次にこれを共役勾配法と比較する。共役勾配法では修正方向ベクトルは式(13)によって計算される。
式(8)から
である。式(25)と式(26)から
式(13)から
これは式(15)から
これと、![]() が正値であることから
が正値であることから
が成り立ち、共役勾配法の解の更新によって、 最急降下法よりも厳密解に近い解が得られ、効率がよい方法だといえる。